
首先,歡迎你來到演算法和資料結構系列文章的倒數第二篇,應該吧???凡事都不好說,哈哈。
此篇要介紹複雜許多的dijkstra algorithm(最短路徑演算法),本來這篇會是這個系列的最後一篇(又是太天真),但礙於內容長度的關係,就被拆成兩篇來寫,除了閱讀時間和篇幅不至於長到讓你棄讀或是直接放棄寫code(脫離
此篇幅大至分成
- 데이크스트라시
- 文字流程解說
- 데이크스트라 부호
- 圖解流程
데이크스트라
데이크스트라시
dijkstra這個演算法是用來在graph資料結構中找到任意起點到任意點的最短路徑。
在這個演算法中,我們會有三個class,分別是
- node(value: 節點值、visited: 節點是否拜訪、edges: 存放該節點鄰近節點的陣列、distancefromstartnode: 該節點離起點的距離、previous: 該節點的上一個節點,以及一個用來增加該節點鄰近節點的方法addedges)
- edges(node: 鄰近節點名稱、weight: 到該節點所需距離)
- minheap(values: 存放節點陣列,以及三個方法,enqueue: 加入節點並排列陣列符合minheap資料結構、dequeue: 拿出、移除陣列中最短路徑節點後並重新排列該陣列為minheap資料結構、minheapify: 確保陣列保持在
最後我們會有一個dijkstra函式用來得出任意起點到各個點的最短路徑,以及一個getshortpathinf輔助函式用來取得各點的詳細資訊。
文字流程解說
- 首先我們會先建立graph的資料結構(line21~46)。
- 接著我們會call dijkstra function,並且給他一個任意起始點。
- 再來將我們的節點都加入到minheap class的陣列(values)當中。
- 「데큐」「MinHeap 값」「전류노드」
- 接下來我們會用minheap values的長度做為條件去執行while loop拜訪每個除了起點之外的節點,並依據條件執行賦值或重新賦值的動作,最後得到每個節點離我們定義起點的距離。
데이크스트라 부호
圖解流程

step1,我們預設起點為a且離起點距離為0,其他未拜訪的節點離起點a的距離我們都不知道所以將它預設為infinity。

단계2de디큐(dequeue)A(StartNode에서 가장 작은 거리),並拜訪a的兩個鄰近節點b、c並且分別將a到b、c的距離賦予給b、c兩個節點的離起點距離都為2(distancefromstartnode)인피니티 2(nearnorNode.StartNode로부터의 거리 = d2 + d3)

step3,再用dequeue取出目前離起點的最短距離節點b(smallest distancefromstartnode)來拜訪(b、c距離都是一樣我們就先挑b來做),b分別有d、e兩個鄰近節點,分別將d、ENFS(Infinity)는 3X6 (nearnorNode.StartNode로부터의 거리 = (d2 + d3))입니다.

단계 4 deue取quequequeue(((((C(StartNode에서 가장 작은 거리)來拜訪,c分別有d、f兩個節點,首先,先檢查c點離起點的距離(d2)加上c到d的距離(d3)是否有大於d離起點的距離(d1),發現沒有,
離F離F離인피니티改4(NearborNode.StartNode로부터의 거리 =d2 + d3))

5단계 디큐(Dequue)D(StartNode에서 가장 작은 거리)來拜訪,d分別有e、f兩個節點。
先檢查e離起點的距離(d2)加上d到e的距離(d3)是否有大於e離起點的距離(d1),發現有,更動e離起點的距離為5(distancefromstartnode)。
再來檢查f點離起點的距離(d2)加上d到f的距離(d3)是否有大於f離起點的距離(d1),發現沒有,不更動f點離起點的距離(distancefromstartnode)
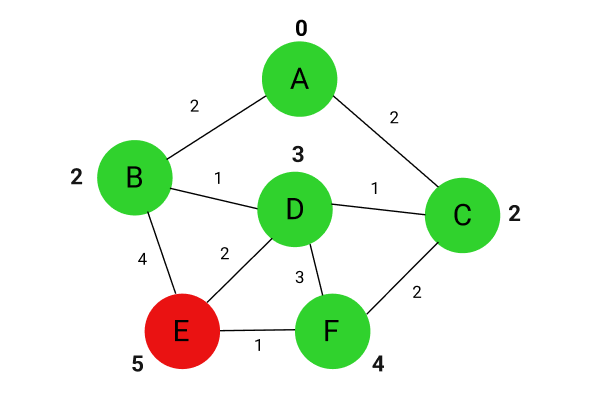
Step6,dequeue(디큐)F(StartNode에서 가장 작은 거리),檢查e節點離起點的距離(d2)加上f到e的距離(d3)是否有大於e點離起點的距離(d1),發現沒有,不更動e點離起點的距離(distancefromstart

Step7,dequeue取取(E(시작노드로부터 가장 작은 거리)也是最後一個節點,該節點沒有其他未拜訪節點,迴圈結束,得出a點到所有點之間的最短路徑。
以上就是整個dijkstra algorithm的整個運作流程圖解。
dijkstra的核心是在每次檢查、賦值後,再用dequeue取出最短距離節點,而dequeue除了會排除每一次的最短路徑節點外,還會再執行一次minheapify確保下一次dequeue取到的節點還會是離起點最短距離的節點,這樣就可以確保由
結語
dijkstra是一個較為複雜的演算法,要理解這個演算法,就必須了解queue資料結構、minheapify的排列方式,以及他是如何使用兩者搭配他自己的核心邏輯去取得我們要的結果。
下一篇要幫大家介紹dynamic programing(動態規劃),下一篇見摟~
喜歡別忘了clap起來~謝謝
'javascript' 카테고리의 다른 글
| Nullish 병합 연산자(?) (0) | 2022.01.11 |
|---|---|
| Javascript에서 Promise 개체의 기본 제공 메서드 (0) | 2022.01.11 |
| Javascript의 O.O. (0) | 2022.01.11 |
| Apaitu Async Waiting, Promise, Callback — Handling Asyncronus javascript #1. (0) | 2022.01.11 |
| Angular 11 및 가 포함된 온라인 상점을 개발합니다.넷 코어 5 (0) | 2022.01.11 |




댓글